Title: A CNN Regression Approach for Real-Time 2D/3D Registration Paper Link
Authors: Shun Miao, Z. Jane Wang, Rui Liao
Association: Department of Electrical and Computer Engineering, University of British Columbia, Vancouver, Canada
Submission: May 2016
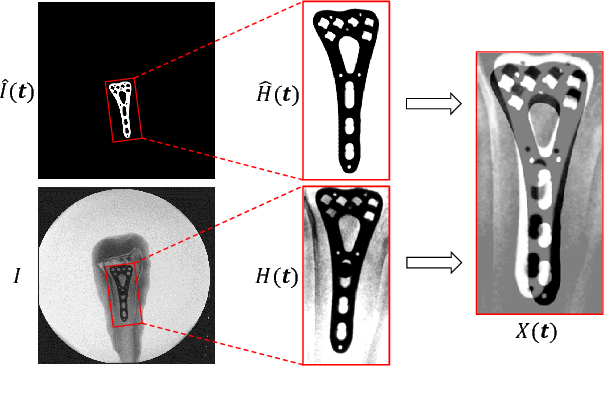
Image registration is a key component for medical image analysis to provide spatial correspondences.
…………………………………………………………………………………………………………………
»> Background of Deep Learning in Medical Image Analysis
»> A Review: Robot-Assisted Endovascular Catheterization Technologies:
…………………………………………………………………………………………………………………
»> Image Registration Basic Knowledge
»> Image Registration Literature Review
»> Slice-To-Volume Medical Image Registration Background
…………………………………………………………………………………………………………………
Contributions
(1) A CNN regression approach, referred to as Pose Estimation via Hierarchical Learning (PEHL), is proposed to achieve real-time 2-D/3-D registration with a large capture range and high accuracy.
(2) to train CNN regressors to recover the mapping from the DRR and X-ray images to the difference of their underlying transformation parameters.
mapping is highly complex and training regressors to recover the mapping is far from being trivial (unimportant)
(3) First simplifying the non-linear relationship using the following three algorithmic strategies: Localimage residual(LIR), Parameter space partitioning (PSP), Hierarchical parameter regression (HPR)
(4) Then capturing the mapping using CNN regressors with a strong non-linear modeling capability.

Digitally Reconstructed Radiograph (DRR)
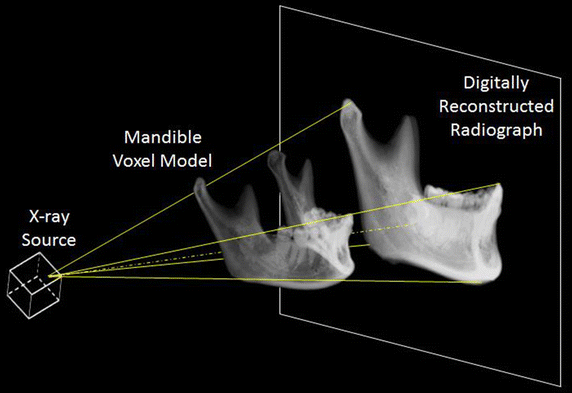


Motivation
(1) Intensity-based methods are known to be able to achieve high registration accuracy — “A comparison of 2D-3D intensity-based registration and feature-based registration for neurointerventions,” in Proc. MICCAI, 2002, two major drawbacks: (1) long computation time (2) small capture range (because intensity-based methods involve a large number of evaluations of the similarity measure, each requiring heavy computation in rendering the DRR)
(2) the similarity measures to be optimized in Intensity-based methods often highly non-convex, the optimizer has a high chance of getting trapped into local maxima, which leads to a small capture range of these methods.
3-D Transformation Parameterization
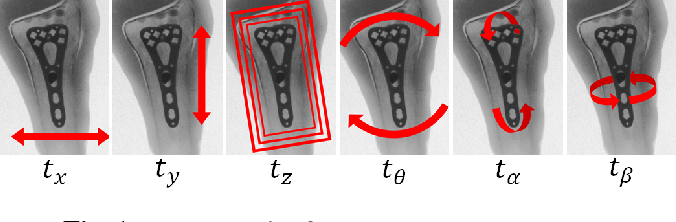 they parameterize the transformation by 3 in-plane and 3 out-of-plane transformation parameters
they parameterize the transformation by 3 in-plane and 3 out-of-plane transformation parameters
in-plane transformation parameters:2 translation parameters and 1 rotation parameter. The effects of in-plane transformation parameters are approximately 2-D rigid-body transformations.
Out-of-plane transformation parameters: 1 out-of-plane translation parameter, and 2 out-of-plane rotation parameters. The effects of out-of-plane translation and rotations are scaling and shape changes, respectively.
2-D/3-D Registration
The inputs for 2-D/3-D registration are:
- a 3-D object described by its X-ray attenuation map (衰减图)
- an X-ray image, where denotes the unknown ground truth transformation parameters
- initial transformation parameters.
The 2-D/3-D registration problem can be formulated as a regression problem, where:

Problem 1: As feature depends on transformation parameters, the target mapping could vary significantly as changes, which makes it highly complex and difficult to be accurately recovered.
Solution 1: extracting a feature that is sensitive to the parameter residuals (残差) and is insensitive to the parameters. Such feature is referred to as pose-index feature.
Local Image Residual 1
Calculation of Local Image Residual:

Extraction of 3-D Points: (The 3-D points used for calculating the LIR feature are extracted separately for each zone in two steps)
- 3-D points that correspond to 2-D edges are extracted as candidates. (the candidates are extracted by thresholding pixels with high gradient magnitudes in a synthetic X-ray image) (i.e., generated using DRR) with and at the center of the zone –> back-projecting them to the corresponding 3-D structures.
find the dominant 3-D structure corresponding to the gradient in the X-ray image
- the candidates are filtered so that only the ones leading to LIR satisfying (7) and also not significantly overlapped are kept.
Hierarchical Parameter Regression

CNN Regression Model
Two challenges:
-
it needs to be flexible enough to capture the complex mapping from X(t,It+t’) to t’
-
it needs to be light-weighted enough to be forwarded in real-time and stored in Random-Access Memory (RAM). Managing memory footprint is particularly important because regressors for all zones (in total 324) need to be loaded to RAM for optimal speed.
Structure of the CNN regression model.
The input of the regression model consists of N channels, corresponding to N LIRs.
Structure of the CNN applied for each input channel.
The CNN Structure: consists of five layers, including two 55 convolutional layers (C1 and C2), each followed by a 22 max-pooling layers (P1 and P2) with stride 2, and a fully-connected layer (F1) with 100 Rectified Linear Unit (ReLU) activations neurons. The feature vectors extracted from all input channels are then concatenated and connected to another fully-connected layer (F2) with 250 ReLU activations neurons. The output layer (F3) is fully-connected to F2, with each output node corresponding to one parameter in the group. Since the input channels have the same nature, i.e., they are LIRs at different locations, the weights in the CNNs are shared to reduce the memory footprint by times.
Loss: The objective function to be minimized during the training is Euclidean loss:

Performance
Instead of regressing the 6 parameters together, which makes the mapping to be regressed more complex as multiple con- founding factors are involved, they divide them into the following 3 groups, and regress them hierarchically:
• Group 1: In-plane parameters the easiest to be estimated, because they cause simple while dominant rigid-body 2-D transformation of the object in the projection image that are less affected by the variations of the parameters in the other two groups.
• Group 2: Out-of-plane rotation parameters • Group 3: Out-of-plane translation parameter most difficult one to be estimated, because it only causes subtle scaling of the object in the projection image. The difficulty in estimating parameters in Group 2 falls in-between.