Title: Spatial Transformer Networks Paper Link
Authors: Max Jaderberg, Karen Simonyan, Andrew Zisserman, Koray Kavukcuoglu
Association: Google DeepMind, London, UK
Submission: Feb 2016
…………………………………………………………………………………………………………………
»> Background of Deep Learning in Medical Image Analysis
»> A Review: Robot-Assisted Endovascular Catheterization Technologies:
…………………………………………………………………………………………………………………
»> Image Registration Basic Knowledge
»> Image Registration Literature Review
»> Slice-To-Volume Medical Image Registration Background
…………………………………………………………………………………………………………………
Contributions

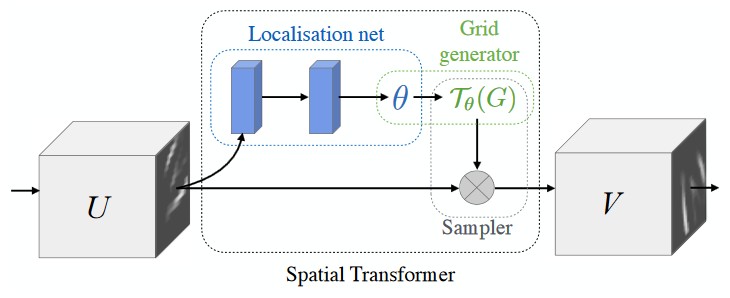
Spatial Transformer Networks (STNs)
The Spatial Transformer mechanism addresses the issues above by providing Convolutional Neural Networks with explicit spatial transformation capabilities. It possesses 3 defining properties that make it very appealing.
modular: STNs can be inserted anywhere into existing architectures with relatively small tweaking (对…稍作调整).
differentiable: STNs can be trained with backprop allowing for end-to-end training of the models they are injected in.
dynamic: STNs perform active spatial transformation on a feature map for each input sample as compared to the pooling layer which acted identically for all input samples.

The Spatial Transformer module consists in three components:
1. localisation network
[goal] spit out the parameters θ of the affine transformation that’ll be applied to the input feature map.
[input] feature map U of shape (H, W, C)
[output] transformation matrix θ of shape (6,)
[architecture] fully-connected network or ConvNet
2. grid generator

[goal] to output a parametrised sampling grid, which is a set of points where the input map should be sampled to produce the desired transformed output.
[architecture]

3. sampler
[goal] To perform a spatial transformation of the input feature map, a sampler must take the set of sampling points Tθ(G), along with the input feature map U and produce the sampled output feature map V.
[architecture]
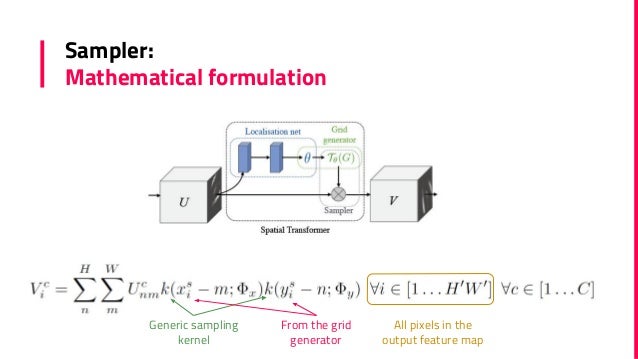
It is also possible to use spatial transformers to downsample or oversample a feature map, as one can define the output dimensions H’ and W’ to be different to the input dimensions H and W. However, with sampling kernels with a fixed, small spatial support (such as the bilinear kernel), downsampling with a spatial transformer can cause aliasing effects.
Performance


Reference
Spatial transformer networks SLIDESAHRE link
Deep Learning Paper Implementations: Spatial Transformer Networks: