Title: Anatomically Constrained Neural Networks (ACNN) Application to Cardiac Image Enhancement and Segmentation Paper Link
Authors: Ozan Oktay
Association: Biomedical Image Analysis Group, Imperial College London
Submission: 2017
Motivation
CNN based segmentation it is not obvious how to incorporate such prior knowledge. State-of-the-art methods operate as pixel-wise classifiers where the training objectives do not incorporate the structure and inter-dependencies of the output.
we propose a generic training strategy that incorporates anatomical prior knowledge into CNNs through a new regularisation model, which is trained end-to-end. The new framework encourages models to follow the global anatomical properties of the underlying anatomy (e.g. shape, label structure) via learnt non-linear representations of the shape
Contributions
(0) learn anatomical shape variations from medical images we propose a generic and novel technique to incorporate priors on shape and label structure into NNs for medical image analysis tasks. In this way, we can constrain the NN training process and guide the NN to make anatomically more meaningful predictions
(1)
(2)
(3)
(4)
Problem 1
The cross-entropy loss function operates on individual pixel level class predictions, which does not guarantee global consistency and plausible anatomical shapes even though the segmentation network has a receptive field larger than the size of structures to be segmented. This is due to the fact that back-propagated gradients are parametrised only by pixel-wise individual probability divergence terms and thus provide little global context.
Solutions
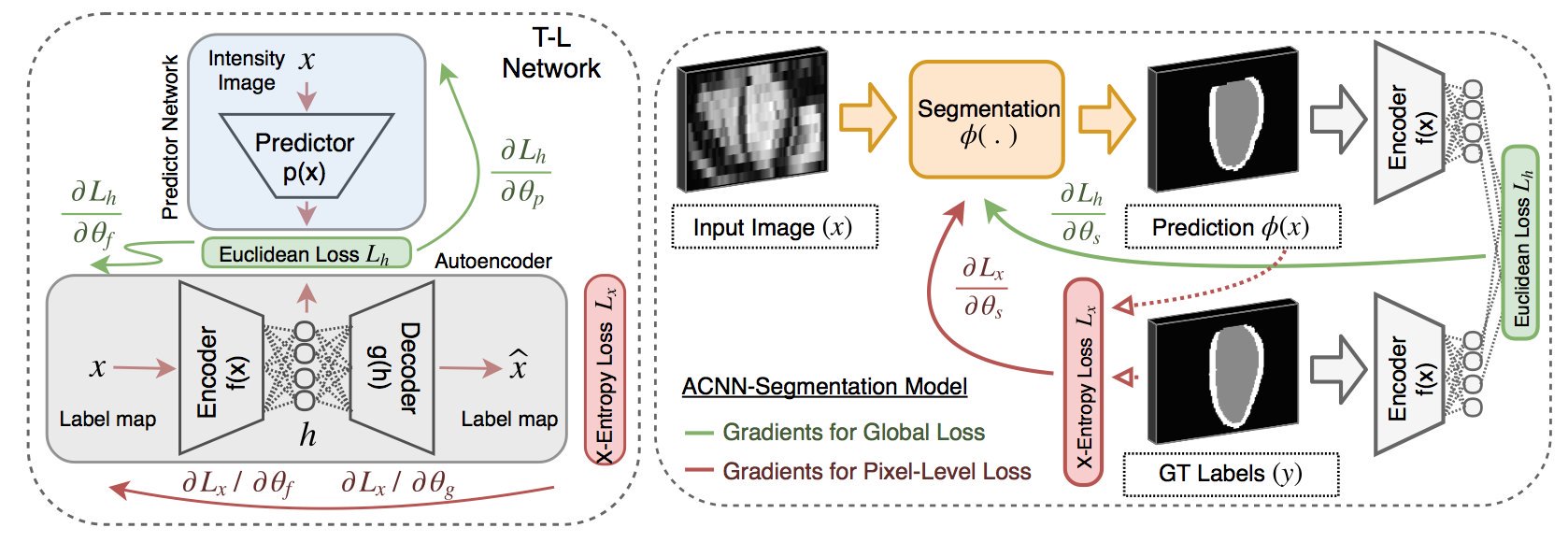
class prediction label maps are passed through the AE to obtain a lower dimensional (e.g. 64 dimensions) parametrisation of the segmentation and its underlying structure [40]. By performing AE-based non-linear lower dimensional projections on both predictions and groundtruth labels, as shown in Fig. 4, we can build our ACNN
Methods

Loss function
consisting of two components:
- penalizes differences in appearance L_sim
And set L_sim to the negative local cross-correlation of M(φ) and F.

- penalizes local spatial variations in φ L_smooth

Performance
